Letzte Änderung am 9. Januar 2024 by Christoph Jüngling
Kürzlich hatte ich mal wieder ein Seminar “Excel Einführung” zu geben. Es war ein spontaner Einsatz, um den ich gebeten wurde, weil ein Kollege wegen Krankheit ausgefallen war. Dummerweise hatte ich nicht bemerkt, dass ich zu diesem Kurs von dem Bildungsträger noch keine Unterlagen bekommen hatte. So habe ich mich gewohnheitsmäßig darauf verlassen, vor Ort über die Cloud an die Unterlagen zu kommen, was dann leider nicht funktioniert hat. Keine Unterlagen heißt: Keine Powerpoint-Präsentation und keine Übungsdateien. So blieb mir nichts anderes übrig als zu improvisieren.
Ich entschied mich für eine allgemeine Kfz-Kosten-Kalkulation. Mir schien (und scheint immer noch), dass dies nicht allzu schwierig sein sollte, da man mit ein paar Grundrechenarten auskommen würde. Keine komplizierten Formeln also, und außer “SUMME” auch keine Excel-Funktionen.
Das sollte einem Anfängerkurs angemessen sein. Dachte ich. Ich habe mich selten so geirrt.
Als erstes schlug ich vor, eine einfache Kalkulation aufzubauen, die davon ausgeht, dass man alle statistischen Daten bereits kennt. Im weiteren Verlauf wollte ich dann eine zusätzliche Tabelle mit fiktiven Tankvorgängen aufbauen und deren Summen in diese Kalkulation übernehmen.
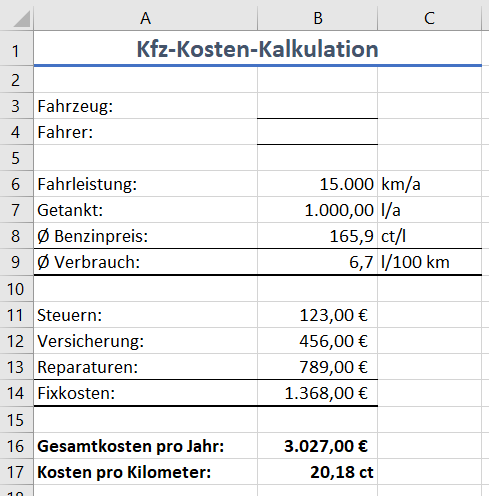
Neben reinen Eingabefeldern für den Namen des Fahrzeugs und des Fahrers sollte die jährliche Fahrleistung, die dafür getankten Liter und der durchschnittliche Benzinpreis (mit dem Sonderzeichen Ø) erfasst werden, zunächst mit Fantasiewerten. Die Einheiten dieser Zahlen haben wir zunächst in separaten Zellen hingeschrieben, so dass das Zahlenformat aus den Standardformaten ausgewählt werden konnte. Als Erweiterung war dann geplant, diese durch benutzerdefinierte Zahlenformate zu ersetzen.
Nun sollte der durchschnittliche Verbrauch in “Litern pro 100 km” berechnet werden. Das scheiterte zunächst daran, dass niemand die Formel dafür kannte. Ich half also aus mit “Liter mal hundert geteilt durch Kilometer”, und baute am Screen die Formel auf: “Gleichheitszeichen das da Stern 100 Schrägstrich das da“. Die beiden “das da” waren jeweils Mausklicks auf die betreffende Zelle, wodurch in Excel die Adresse der angeklickten Zelle in die Formel übernommen wird. Im Beispiel entstand also die Formel =B7*100/B6. Das erste Problem war die anscheinend ernstgemeinte Frage eines Teilnehmers, ob man denn nicht auch Kilometer durch Liter rechnen könne und am Ende dann durch 100 teilen, das sei doch im Grunde dasselbe. “Nein”, sagte ich, “Liter durch Kilometer ergibt einen anderen Wert als Kilometer durch Liter“. Der Teilnehmer glaubte das nicht.
Dann ging es weiter mit Eingabefeldern für Steuern, Versicherung und Reparaturen, deren Werte durch den Klick auf das betreffende Symbol im Buchhaltungsformat zu formatieren waren. Deren Summe wurde per “AutoSumme” ermittelt. Das klappte.
Zum Schluss sollten dann die Gesamtkosten pro Jahr und danach auch die Kosten pro Kilometer ermittelt werden. Für die Gesamtkosten pro Jahr mussten also die getankten Liter mit dem Literpreis multipliziert werden, dazu wurde dann die bereits ermittelte Summe der Fixkosten addiert. Zunächst ergab das mit den Zahlen des vorliegenden Beispiels die überraschend hohe Summe von 167.268 € pro Jahr, die sich niemand erklären konnte. Ich wies darauf hin, dass der Benzinpreis in “Cent pro Litern” angegeben sei, unser Ergebnis aber in Euro berechnet werden solle. Unverständliche Blicke waren die Folge. Dass man von Cent auf Euro kommt, indem man den Wert einfach durch 100 teilt, war offenbar schon höhere Mathematik, aber gut, ich gab auch diesen Hinweis. Dadurch entstand ein erschwinglicher Betrag von etwas über 3000 Euro pro Jahr.
Dann kam die Frage nach den Kosten pro Kilometer. Na ja, “Gesamtkosten geteilt durch die gefahrenen Kilometer” ergänzte ich. Man rechnete, es ergaben sich “0,20 ct”. Gut. Fertig, endlich!
Oder nicht? Wenn da eine Zahl steht und keine Fehlermeldung, so denken anscheinend viele, dann wird das wohl richtig sein. “Null Komma zwanzig Cent?”, fragte ich. “Ist das realistisch?” Nein, wohl eher nicht. Erst war das Auto zu teuer, nun plötzlich zu billig. Und wieder war da die Hürde, diesmal aber musste “von Euro auf Cent” umgerechnet werden. Gerade erst erklärt, schon wieder vergessen. “Mit 100 malnehmen”, half ich. =B16/B6 stand als Formel da, aber wie multipliziert man denn mit 100? “Stern 100 dahinter schreiben”, empfahl ich und erklärte (nochmal?) die Rechenzeichen der vier Grundrechenarten. Na das ging dann. Nun betrug der Preis pro Kilometer ca. 20 ct. Schon realistischer.
Fassen wir zusammen
In diesem Kurs ging es nicht um Partielle Differentialgleichungen, Polynomdivision, oder Integralrechnung. Die im Grunde einzigen mathematischen Herausforderungen des Tages waren die Grundrechenarten. Sind Berechnungen wie “Liter mal 100 durch Kilometer” und “von Cent auf Euro” bzw. umgekehrt wirklich so schwer? Sollten erwachsene Leute mit einer normalen Schulbildung bei solchen einfachen Aufgaben wirklich kapitulieren? Wie ist das dann erst mit Dreisatz oder einfacher Prozentrechnung? Und wenn das tatsächlich so sein sollte, wieso geht man dann in einen Excel-Kurs?
Als ich das im Familienkreis erzählte, zitierte meine Tochter eine Kollegin: “Bei Excel muss man nicht rechnen können, das macht Excel schon selbst.” Na dann ist ja alles klar.
Ist es meine Aufgabe als Excel-Dozent, den Menschen zunächst das Rechnen beizubringen? Ja, vielleicht. Und es ist gut möglich, dass wir unsere Einstellung zu dem, was Allgemeinbildung ist, wohl überdenken sollten. Aber dazu müsste für einen Excel-Grundkurs deutlich mehr Zeit eingeplant werden. An mir soll es nicht scheitern, aber welcher Arbeitgeber würde für so einen Kurs bezahlen?
Weiter geht’s in Gedanken … (2)
2 Kommentare
Danke für diesen Artikel. Weitgehend mache ich ähnliche Erfahrungen, insbesondere mit Leuten, die beispielsweise in sozialen Berufen arbeiten. Die sind eben nicht technikaffin, haben keinen Spaß an abstraktem und logischem Denken und die Erinnerung an Mathe in der Schule kann zu einer Retraumatisierung führen.
Dennoch bieten gerade diese Menschen für mich die Chance zur Erweiterung meiner soft-skills:
Wie weit entwickelt ist meine Empathie?
Wie kreativ kann ich erklären?
Wie kann ich große Unterschiede in den Vorkenntnissen überbrücken?
Autor
Dass es Unterschiede gibt, habe ich auch bemerkt, sind keineswegs alle so wie oben beschrieben (siehe den zweiten Artikel mit diesem Thema). Ich fürchte, dass es nicht nur mit einer kreativeren Erklärung lösbar ist, sondern viel tiefer angesetzt werden muss. Doch geht das in einem Standard-Excel-Kurs?