 Spätestens seit das Corona-Virus in Deutschland wütet ist ein Begriff aus der Mathematik in aller Munde: Die Exponentialfunktion, oder auch das exponentielle Wachstum. Auch wenn es im Kern kein IT-Thema ist, könnte man es doch mal im Rahmen dieses Blogs beachten. Dazu habe ich noch zwei nette Geschichten, die ich als Kind schon erzählt bekam, die anscheinend heute kaum noch jemand kennt.
Spätestens seit das Corona-Virus in Deutschland wütet ist ein Begriff aus der Mathematik in aller Munde: Die Exponentialfunktion, oder auch das exponentielle Wachstum. Auch wenn es im Kern kein IT-Thema ist, könnte man es doch mal im Rahmen dieses Blogs beachten. Dazu habe ich noch zwei nette Geschichten, die ich als Kind schon erzählt bekam, die anscheinend heute kaum noch jemand kennt.
In diesem Artikel
Wachstum? Kennt man doch!
Jeder Kaufmann, Betriebs- oder Volkswirt kennt wohl den Begriff Wachstum, und in aller Regel verbindet nicht nur diese Klientel damit auch eine gewisse Liebe. “Über sich selbst hinauswachsen” ist dabei eher eine Metapher, da dem körperlichen Wachstum gewisse Grenzen gesetzt sind. Aber in Unternehmen (Volkswirtschaften) heißt es gern, man müsse wachsen, da man ansonsten kaputt gehe. Doch nicht immer ist grenzenloses Wachstum etwas Positives, fragt mal einen Biologen!
Denn das ist genau eines der beiden Probleme: Viren und Bakterien (und auch Krebszellen) neigen dazu, sich zu vermehren. Und wenn dies ungehindert passiert, wird über kurz oder lang der befallene Organismus zerstört, das Lebewesen stirbt. Das gilt im Prinzip allerdings nicht nur für die kleinen Dinge, auch das Bevölkerungswachstum funktioniert ähnlich – und kann ein ebensolches Problem werden, dann natürlich für den Planeten. Was kann man dagegen tun?
Das andere Problem ist das Verständnis.
Was ist Wachstum?
Eigentlich ist es ganz einfach: Wachstum ist, wenn irgendwas zunimmt. Wenn ich also jedes Jahr ein wenig schwerer werde, ist das auch Wachstum, aber kein erstrebenswertes, und hoffentlich hört das auch irgendwann mal auf!
Dabei gibt es verschiedene Möglichkeiten. Eine Möglichkeit ist das lineare Wachstum. Dabei nimmt in gleichen Zeitabständen die Gesamtzahl der Elemente in immer gleichen Portionen zu. Und dann gibt es da noch das exponentielle Wachstum, bei dem die Zunahme selbst zunimmt. Also nicht nur “immer mehr”, sondern quasi “immer mehr mehr”. Das klingt verrückt, aber das ist genau das, was gerne vergessen wird.
Exponentielles Wachstum
Exponentielles Wachstum ist laut Wikipedia definiert als ein mathematisches Modell für einen Wachstumsprozess, bei dem sich die Bestandsgröße in jeweils gleichen Zeitschritten immer um denselben Faktor vervielfacht. Und das ist der wesentliche Unterschied zum oben beschrieben linearen Wachstum. Dort wächst die Bestandsgröße in jeweils gleichen Zeitschritten immer um denselben Betrag. Verstanden?
Vielleicht. Aber wie kann man sich das vorstellen? Dazu zwei Geschichten.
Der Seerosenteich
 Als Kind kannte ich ein Rätsel, dessen Bedeutung für die Mathematik mir erst viele Jahre später bewusst wurde. Es verdeutlichte aber, wie schwierig es sein kann, sich ein nichtlineares Wachstum vorzustellen.
Als Kind kannte ich ein Rätsel, dessen Bedeutung für die Mathematik mir erst viele Jahre später bewusst wurde. Es verdeutlichte aber, wie schwierig es sein kann, sich ein nichtlineares Wachstum vorzustellen.
Es geht um einen Teich vor dem Dorf, auf dem eine einzelne Seerose blüht. Als die Kinder am nächsten Tag wieder dort spielten, sahen sie bereits zwei Seerosen, und am Tag darauf waren es vier. Jeden weiteren Tag verdoppelte sich die Anzahl der Seerosen, bis der Teich komplett davon bedeckt war. Die Kinder haben genau mitgezählt, und es war am 30. Tag, dass der Teich voller Seerosen war.
Und dann kam die Frage: Am wievielten Tag war der See zur Hälfte bedeckt?
Wir Kinder – und ich war da keinesfalls eine Ausnahme – sagten natürlich spontan “am 15. Tag”, denn das schien klar: Die Hälfte von 30 ist 15. Aber so einfach ist es leider nicht. Denn wenn jeden weitere Tag doppelt so viele Seerosen auf dem Teich sind, heißt das umgekehrt doch, dass am Vortag nur die Hälfte davon zu sehen war. Und der Vortag des 30. ist der 29., und das ist dann folglich der Tag, an dem der See halb bedeckt war.
Nun ist in diesem Rätsel der Faktor, um den die Bestandsgröße (Anzahl der Seerosen) in jedem Zeitabschnitt (Tag) wächst, eine simple 2. Und es zählt in diesem Rätsel nur die Gesamtzahl der Seerosen. Beim nächsten Beispiel ist das ein klein wenig anders.
Der schlaue Wesir
 Die zweite Geschichte schildert ein ähnliches Prinzip, und ich kann sie leider nur noch aus der Erinnerung erzählen. Daher weiß ich nicht, wie es zu der Situation kam, ich kenne nur noch das Ergebnis.
Die zweite Geschichte schildert ein ähnliches Prinzip, und ich kann sie leider nur noch aus der Erinnerung erzählen. Daher weiß ich nicht, wie es zu der Situation kam, ich kenne nur noch das Ergebnis.
In dieser Geschichte ging es um einen Wesir, der seinem Sultan einen großen Dienst erwiesen hat. Der Sultan wollte sich erkenntlich zeigen und stimmte einem Handel zu, den der schlaue Wesir vorgeschlagen hatte. Der Sultan sollte auf das erste Feld eines Schachspiels ein Reiskorn legen, und auf jedes weitere Feld jeweils doppelt so viele Reiskörner wie zuvor. Wenn das letzte Feld des Schachbretts gefüllt ist, so sollte der gesamte Reis dem Wesir gehören.
Wir können uns wohl vorstellen, dass der Sultan bei diesem Handel arm wurde!
Fazit
Das schwierige bei dem Verständnis von exponentiellem Wachstum ist die Geschwindigkeit. Am Anfang scheint es noch recht überschaubar, ob es nun um Seerosen oder Reiskörner ging: Erst 1, dann 2, dann 4, dann 8. Das kann man sich noch vorstellen. Aber dass wir beim 10. Schritt (Tag, Spielfeld) bereits bei etwa 1000 (210 = 1024) und beim 20. Schritt bei über einer Million (220 = 1.048.576) angekommen sind, das kann man schon nicht mehr an den Fingern abzählen.
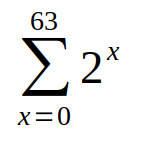 Und in der Geschichte mit dem Wesir kommt noch ein weiterer Aspekt hinzu: Nicht die Zahl der Reiskörner auf dem letzten Spielfeld (263 ≈ 9,2 x 1018, also 9,2 Trillionen), sondern zusätzlich die Summe aller vorherigen Felder ebenfalls.
Und in der Geschichte mit dem Wesir kommt noch ein weiterer Aspekt hinzu: Nicht die Zahl der Reiskörner auf dem letzten Spielfeld (263 ≈ 9,2 x 1018, also 9,2 Trillionen), sondern zusätzlich die Summe aller vorherigen Felder ebenfalls.
Wahrscheinlich gab es auch im gesamten Reich nicht so viele Reiskörner: 18.446.744.073.709.551.615
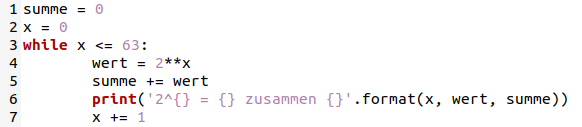
Das habe ich natürlich nicht im Kopf ausgerechnet. So schwierig ist es nicht. Mit einem kleinen Python-Programm lässt sich das schnell ermitteln:
Macht euch ruhig die Mühe, dieses Programm selbst einzutippen und auszuführen! Dann schaut euch die Ergebnisse jeder Zeile genauer an. Ich denke, ihr findet sicher einen Weg, das alles viel einfacher auszurechnen :-)

1 Ping
[…] Wie oft habe ich gehört “das haben wir schon immer so gemacht”! Kennt jemand die Fabel mit dem Seerosenteich? Oder die fatale Fehleinschätzung der Bakterien, die während 100 Generationen auf rapides […]